【人気ダウンロード!】 分数 の 大小 222322-分数の大小 何年生
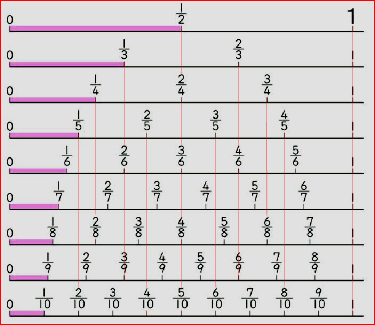
③分数の大小の比較 ④同じ分母の分数のたし算・ひき算 教え方1 1mの長さのテープをもとに分数を使った「はしたの長さの表し方」を教えます。 下の図を見せながら、テープ1mの の長さに気づかせます。 ↓ こたえ 下の図を見せながら、テープ1mの の長さに気づかせます。 ↓↓↓ ※ と に② 「単位分数の このように,テープ図の切れ目と数直線の目盛りの位置を対応させること,また,分数の大小 関係を数直線を用いて考えさせる活動を通して,単位分数の意識や,テープ図という具体的な量(長さ)から, 数の見方へと近づけることができる と考えました。 (6)3年生つまり、数の大小を比べるのに、とても便利な道具です。 だから、数直線をたてに並べれば、 大きさの等しい分数は、一発でわかるということになります。 では、実際の問題で、見ていくことにしましょう。 (問 1) 次の図で、色をぬった部分の大きさは、どれも同じです。 それぞれの大きさ

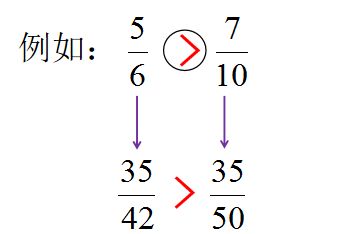
意外に複雑 分数の大小の見分け方6つのパターン 中学受験クルージング
分数の大小 何年生
分数の大小 何年生-無理数の大小比較をするときのコツ 高校生でもわかっていない人多いですが、学校では教えないのでしょうかね。 数の大小比較の基本的な作業は、 数字の世界をそろえてやること です。 整数なら整数どうしで、分数なら分数どうしで、小数なら小数 分割分数のたし算をオセロで考えてみましょう。 すると、 と、「分母+分母」が正しくなってしまいます。 一方、量分数では、1/2m は 1/3m よりも常に大きく(長く)なります。 つまり、量分数は大小比較が可能であり、量分数によって、分数を「大小関係を持った数」として扱えるようになるのです。 3年生の算数, 4年生の算数, 5年生の算数, 算数の基礎, 算数雑学 執筆者: dadandan




大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ
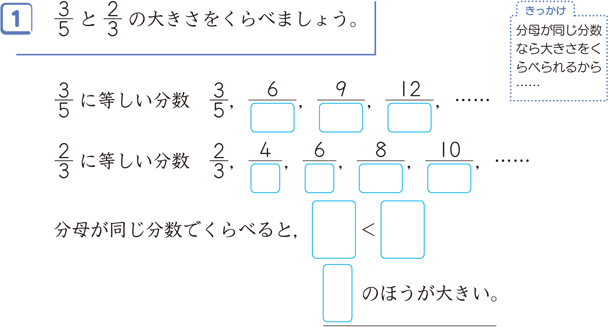
大きく数が違う分数の大小の比べ方が 分かりません。 ⁹⁸³⁄₁₄₁₁と¹⁹²⁄₂₂₄と¹²⁸⁄₅₄₈と¹⁰³⁄₁₁₃と⁸⁄₁₃を 比べたいんですけど、どのようにすれば 簡単に大小を比べることができますか? アドバイスお では分数の大小関係はどう定義されるのかというと、まずは、二つの分数が等しい、つまり (a,b,c,dを整数,bとdは0でないとして) a/b = c/d ということが ad = bc として定義されます。 つまり、「1つ目の分数の分子かける2つ目の分数の分母と、2つ目の分数の分子かける1つ目の分数の分母が等しいときに、1つ目の分数と2つ目の分数は等しい」と、 (大学以上では)定義されるのです。学習のポイント 1より大きい分数を仮分数や帯分数を用いて表し、分数の数直線を表示したり、分数の相等や大小関係を考え学習していきましょう、 1より大きい分数を仮分数や帯分数で表すことを理解しましょう。 「仮分数」「帯分数」
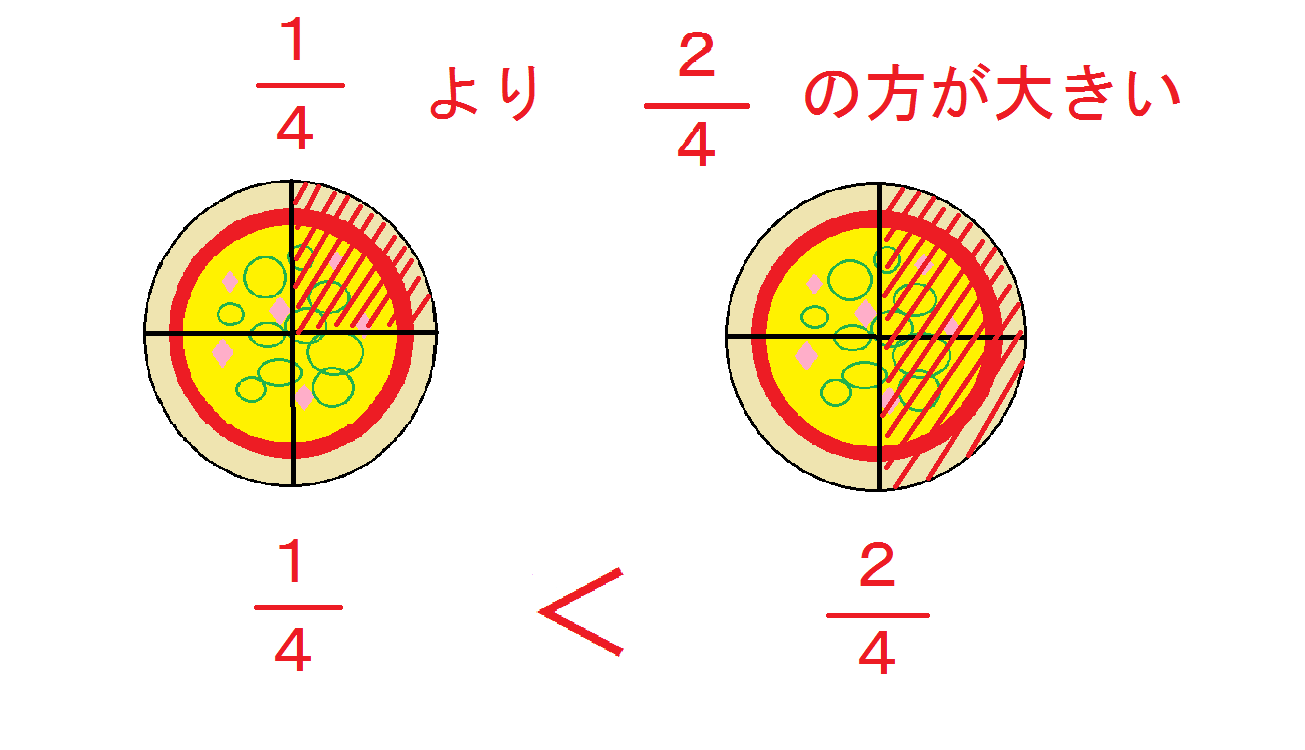
が分数でしたよね! では、その分数どうしでどっちが大きいか? を今回は考えてみましょう! たとえば、4等分したピザを1つとった場合と2つとった場合。 比べてみると、もちろん2つ分の方が多いですよね。 つまり、 分母が同じなら分子が大きい分数の方が大きい という事です! では次。 4等分したうちの1つと、8等分したうちの2つではどうでしょう? 分母が違うのでそのままではア 整数及び小数を分数の形に直したり,分数を小数で表したりすること。 イ 整数の除法の結果は,分数を用いると常に一つの数として表すことができることを理 解すること。 3 子どもの実態(男子15名 女子11名 合計26名) (1)関心・意欲・態度について fùfñg fÛføfÔfÖfø fùfñg fÛføfÔfÖfø fÒföfÿg分数と小数の関係を調べ,大小比較 をする。 (1) 分数の仕組みを調べ,同分母分数の大 小比較をする。 (1) 分数のたし算とひき算の仕方を考 える。 (1)(本時7/9) 分の1のいくつ分で考えれば,分 数で表せるね。 1mや1Lを何等分したいくつ分で 見ればいいね。 身近な長さやかさも分数
正の分数 の中でも このことは n / m を真分数であるとして、1 および n / m の m 倍の数について大小を比較することで確認できる。 一方、1以上となる分数を仮分数(かぶんすう、英 improper fraction )という。分子と分母が同等量(即ち1)か、分子が分母より大きい分数である。例として、少数が含まれている分数を通分する場合には、まず少数の分数を整数の分数になおします。 例えば02/04のような分数は分母・分子に10をそれぞれ掛けて2/4という整数の分数にします。 このままでも通分はできますが約分が可能な場合は約分までやっておくと通分の分数が小さくできます。 2/4は1/2に約分することができます。 あとは通常の通分と同じように分母の最小公倍数を求めて分母を 分数の大きさを比べる 分母の同じ分数の大きさは、分子の大きさを比べればわかります。 と と比べると、 は1つの円を3等分したものが1個、 は3等分したものが2個ですから、もちろん2個の の方が大きいことがわかるわけです。 (左の緑の円) 分母の違う分数は、分子をくらべただけでは大きさがわかりません。 と を比べてみましょう。 (右のオレンジの円) 実際はオレンジの図の



分数大小比较 实际问题分析 网易视频




3种方法来按从小到大的顺序将分数排序
小学生|算数|分数の無料問題集一覧|おかわりドリル このページは、 分数の問題集を一覧で確認できる ページです。 ぴよ校長 いろいろな「分数」の問題を集めているよ! 学年別に問題をまとめているので、学習したい学年の問題を解いてみて下さい 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。分数的基本性质:分数的分子和分母都乘以或都除以同一个不为零的数,所得到的分数与原分数的大小相等。 (b、c不等于零) 分数还有一个有趣的性质:一个分数不是有限小数,就是无限循环小数,像π等这样的无限不循环小数,是不可能用分数代替的。 分数的另一个性质是:当分子与分母同时乘以
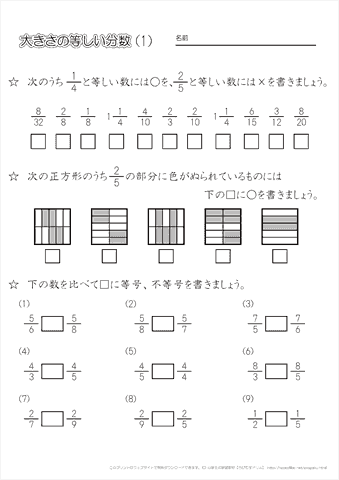



小学4年生の算数 大きさの等しい分数の理解 練習問題プリント ちびむすドリル 小学生




小4算数 分数 の学習プリント 無料ダウンロード 印刷
算数ドリル 分数の大小 № 月日 名前 2つの分数を小数に直して比べなさい。 2つの分数を小数に通分して比べなさい。分数の大きさの比べ方は? 分数の大きさの比較は、 ・分数を小数に直す ・通分する と簡単です。 例えば、1/3と3/8の大きさを、不等号を用いて比較しましょう。 一見、どちらが大きいか分かりません。 そこで分数を小数に変換します。 1/3=1÷3=0333≒033 3/8=3÷8=0375 ですね。 当然、033<0375ですから分数に戻すと「1/3<3/8」だと分かります。 また、1/3と3/8を通分しても分数の大きさ比較ドリル 分数の大きさ比較ドリル 2つの分数を比較して等号または不等号を書きましょう. 2つの値の大きさを比較して,四角の空欄に等号または不等号を書く練習問題です.分数と分数の比較,または分数と小数の比較の設問が選択できます.分数は仮分数,帯分数などを選択できます. 比較する2値を近い値に設定することができます.この選択によっても難易度を調整できます.




如何比较分数的大小 4 步骤



通分のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料
・ 分数の大小比較では分母を揃えて分子で比較すること ・ 色々なタイプの通分の仕方について慣れる 大小比較の等号や不等号の使い方は、何度か触れてきているのでやり出したらすぐ思い出せると思います。 色々なタイプの通分を混ぜているので、その使い分けが難しいところだと思います 基本的には、分子もしくは分母を揃えないと、分数の大きさの比較はやりにくいことが多いです。 分数の大きさを比較するには、分母が同じ分数にすることで比較するやり方が一般的です。 早速例題を使って分数の大きさを比べてみましょう。 例題 どちらの分数のほうが大きいですか。 $$\frac {7} {13},\frac {10} {23}$$ まずは分母を揃えて分数の大きさを比べてみましょう。 分数の分 応用分数の大小比較の問題 問題4.次の $2$ つの分数のうち、どちらが大きいか答えなさい。 (1) $\displaystyle \frac{7}{10} \ , \ \frac{17}{25}$ (2) $\displaystyle 8\frac{2}{15} \ , \ \frac{163}{}$ さあ、ラストの問題は、 分数の大小比較 です。 今まで学んできた知識を活かせば、応用問題だって解けるはず



Juken Act Co Jp
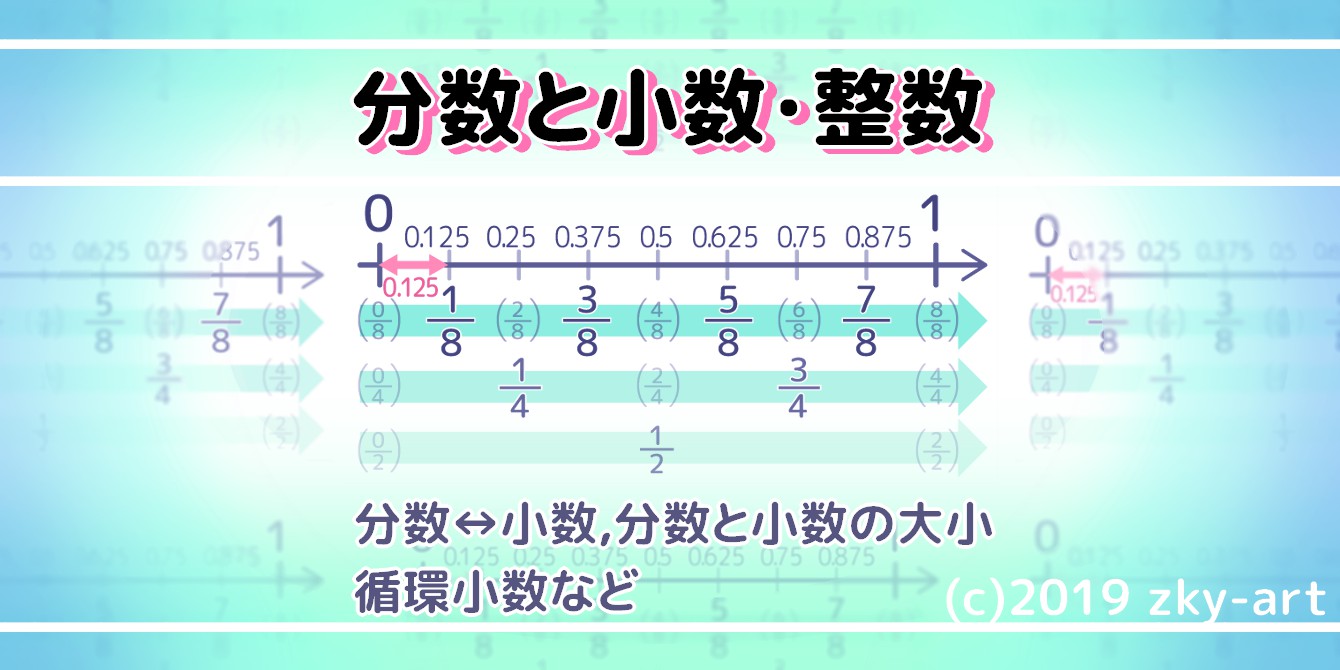



分数を 循環 小数や整数に変換する方法を分かりやすく 大小比較の練習問題も そうちゃ式 分かりやすい図解算数 別館
③等しい分数と分数の大小の意味 ④同分母の分数のたし算とひき算のしかた 教え方1 箱を包んだリボンのそれぞれの長さを調べ、1より大きいはしたの分数を理解させます。そして、真分数と仮分数の意味を教えます。 4本のリボンの長さを比べました。 ②の長さは、1mを2つに等しく分けた1つ 分数の大小を比較する4つの方法 この記事では、分数を比較するうえでの5つの異なる解き方について説明しています。 子どもたちは分数の大小を比較する方法として、以下の4つの方法で比較していると思います。 分母が同じ分数の比較 分子が同じ分数の比較 単位分数の比較 1/2との比較 これらの解き方は、すべて分数の正確な理解に基づいていおり、多くの分数の比較の処理に適してコピーする《 算数 》小学3年生, 小数, 分数 関連記事 小学4年生|算数|無料問題集|小数(100分の1の位まで)×1桁の整数の



授業がんばりmath



Www1 Iwate Ed Jp
分数の大小関係を比較するときには それぞれの数の絶対値を 通分して比較してみることがポイントですね! 3つの大小関係 今までは2つの数の大小関係について考えてきましたが 問題によっては後半の『仕上げ』以降は、分母が等しく分子が異なる分数の大小比較も混ざっていますので、混乱しないで解けるようになるまで十分練習していってください。 まとめpdf「分数8分母で大きさくらべ」 pdf まとめpdfは、下記の16件(全32ページ)のプリント一覧をまとめて表示しますタルトを分数の大きさで提供するお店に通うイチ。あるトリックを使って、安い値段でそのお店のタルトを購入している怪しい男がいた。一度は言い負かされたイチだったが nhk 1500 立てば分数、寝そべれば比 マテマティカ2 割り算・分数・比の三つの表現の関係を考える。 nhk 1500 切って
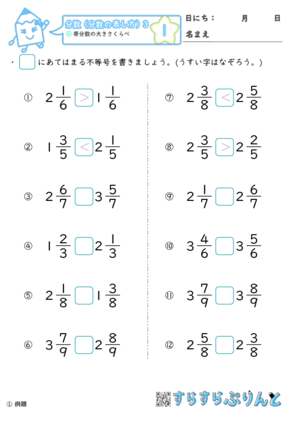



分数 帯分数の大きさくらべ 小学4年算数 無料プリント




大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ
分数の分母は “条件” を意味します。 1/2と1/3を足し合わせるためには、“ 二等分にする ” と “ 三等分にする ” という2つの条件が両立する必要があります。 しかし2/5とは、“五等分にした内の2つ” という意味です。 エクセルで分数の計算する場合は、上記の「分数で足し算や掛け算などの計算をする方法」セクションを参考に、計算してみてください。 このページを見ている人におすすめの商品 Excel 最強の教科書完全版――すぐに使えて、一生役立つ「成果を生み出す」超エクセル仕事術 SB次の2つの数の大小を比べよ。 底が3と9であり、揃っていません。 このままでは大小比較ができないので、まずは底を揃えていきます。 の対数を底3となるよう変形します。 つまり、 と の大小を比較すればよいということになります。 底3は1より大きい




意外に複雑 分数の大小の見分け方6つのパターン 中学受験クルージング



数的処理対策ー資料解釈 分数の大小比較ー 公務員試験受験生を応援します
分数の場合 分母を等しくする. 指数(累乗,累乗根)の場合 底をそろえる r , s が実数で, r > s であるなら, a > 1 のとき, a r > a s 0 < a < 1 のとき, a r < a s 例) 32 3 と 2 2 の大小を比較せよ. 32 3 を累乗の形にすると, 32 3 = 2 5 3 = (2 5) 1通分によって分数の大小をみわける 通分ができるようになれば、分数を比較するとき、数字の大小を見分けられるようになります。たとえば、以下の数字はどちらのほうが大きいでしょうか。 $\displaystyle\frac{2}{5}$、$\displaystyle\frac{3}{8}$ 通分を習っていない場合、この問題を解くこと分数には、「 分母と分子に同じ数をかけ算しても、同じ数でわり算しても、大きさは変わらない 」という性質があります。 特に、 分母と分子を同じ数でわり算して、なるべく小さな数にすることを約分 といいます。 分数はできるだけ約分をするのがマナーです。 分数が出てきたら、いつでも「約分できるかな? 」って考えるようにしましょう。 (例題4) 次の分数を約分しましょう。 分母と分子




すきるまドリル 小学4年生 算数 分数 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント




小数の大小比較 わからないときは10倍や100倍しよう 中学や高校の数学の計算問題
小学5年生の算数 わり算と分数|商分数/分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 ( 1を3等分したものを2つ集めたもの= 2/3 )は3年生で学習します。




小5算数 通分と分数の大小 Youtube




分数比较大小 Pdf
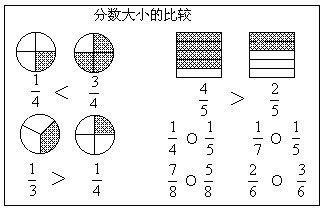



快速判定两分数大小的方法 百度经验




5年生算数 分数の大きさ比べ 通分だけじゃないおもしろさ




分数の大小関係 通分や小数にするのが解き方のコツだ 中学や高校の数学の計算問題




指数の大小比較でどうして何乗かするのですか Clearnote



通分と約分 算数用語集



平方根を含む分数の大小比較についてです 5 1 2と2 3の大小はどのよう Yahoo 知恵袋




世界一分かりやすい算数 小3 分数




分数的大小比较 Ppt下载 牛二ppt




算数 小4 53 大きさの等しい分数 Youtube




動画で学習 1 分数の大きさ 算数



3年算数プリント 分数1



受験生です 数1aの最初の計算が苦手ですルート 分数が同時にある数の大 Yahoo 知恵袋



算数 本当に 分かる という事 分数の大小 通分 エース学院



小学奥数 分数的大小比较 哔哩哔哩 Bilibili




大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ
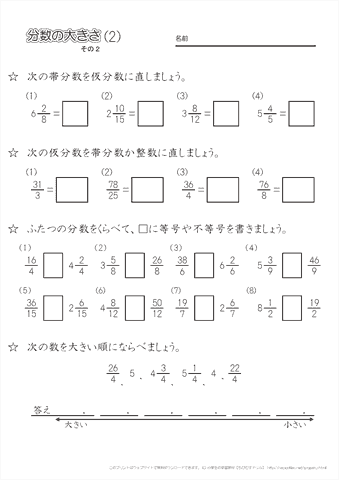



小学4年生の算数 分数の大きさ 2 真分数 仮分数 帯分数の計算 練習問題プリント ちびむすドリル 小学生
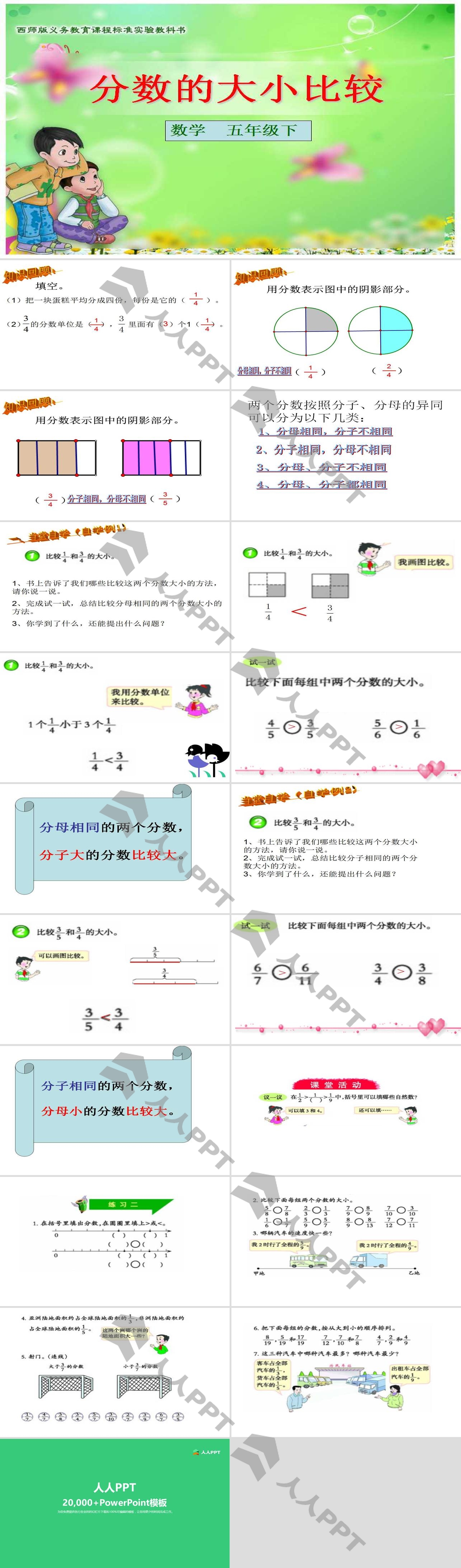



分数的大小比较 分数ppt课件2 Ppt课件下载 人人ppt




分数の大小比較 スクールプレゼンター教材共有サイト スクプレ道場




通分で考える 数の大小 名寄 算数数学教室より



分数の大小の調べ方 算数解法の極意
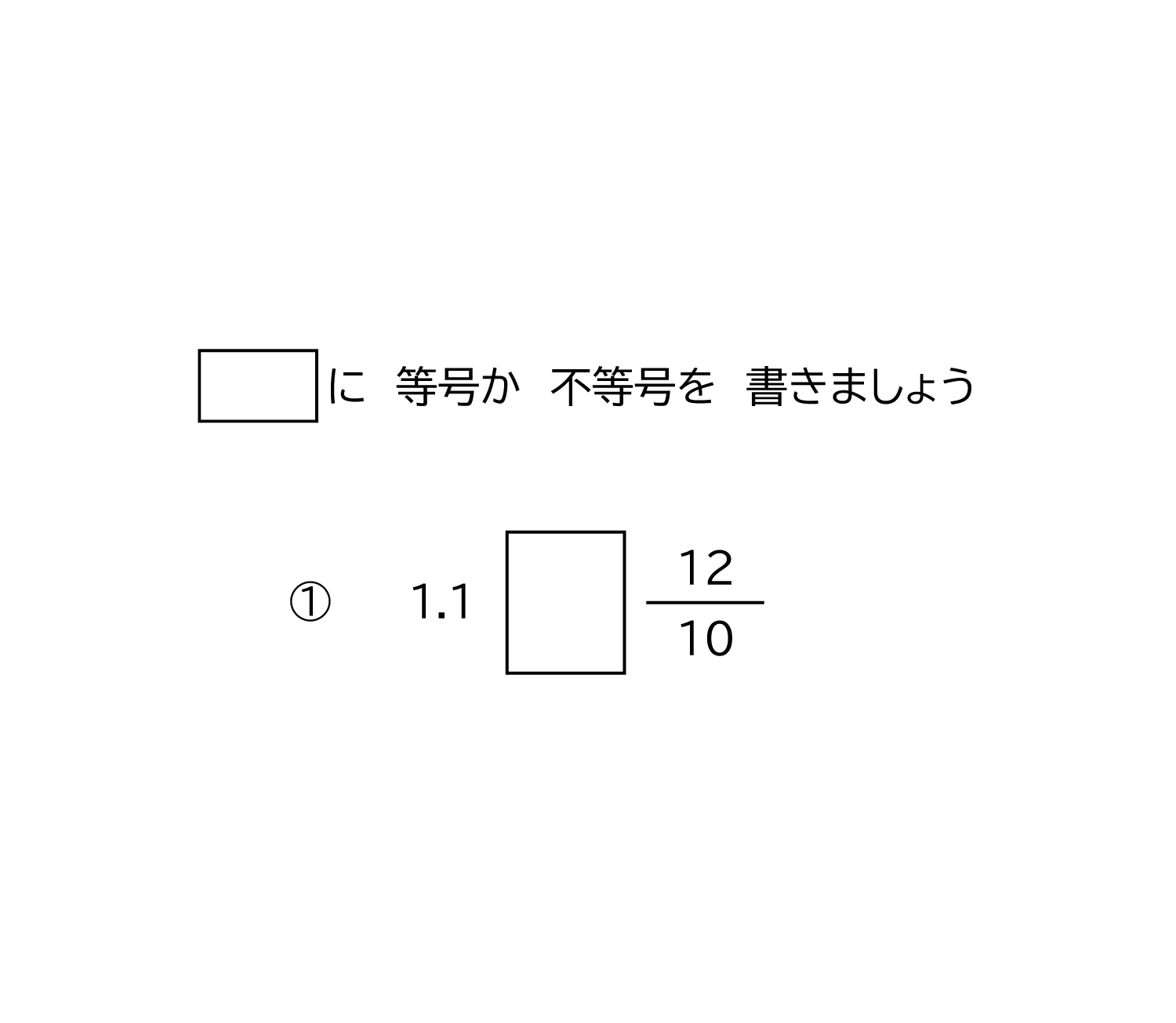



小学3年生 算数 無料問題集 分数と小数の大小 おかわりドリル



Center Gsn Ed Jp
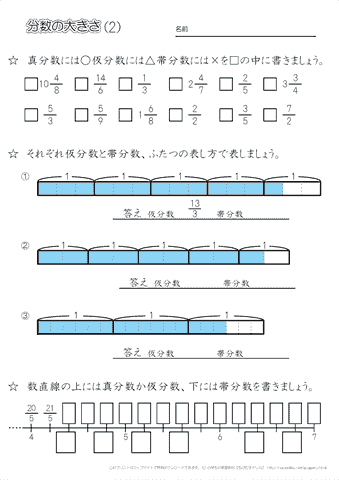



小学4年生の算数 分数の大きさ 1 真分数 仮分数 帯分数の意味 練習問題プリント ちびむすドリル 小学生



3
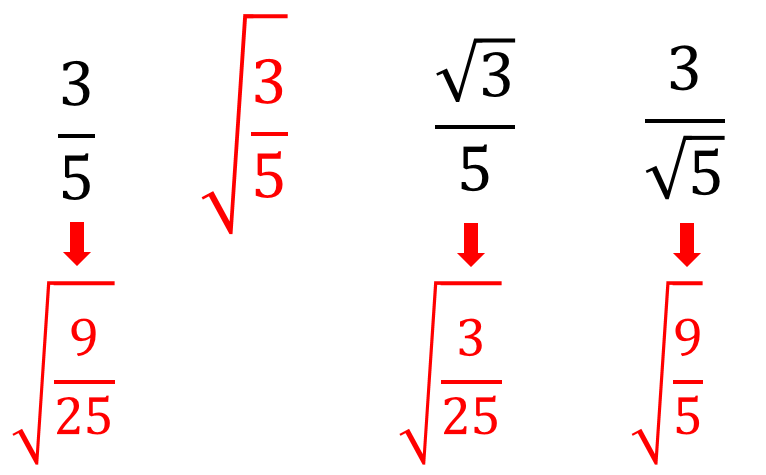



平方根 大小関係を不等号で表す問題を解説 数スタ




分数的大小 分数的意义ppt 第一ppt
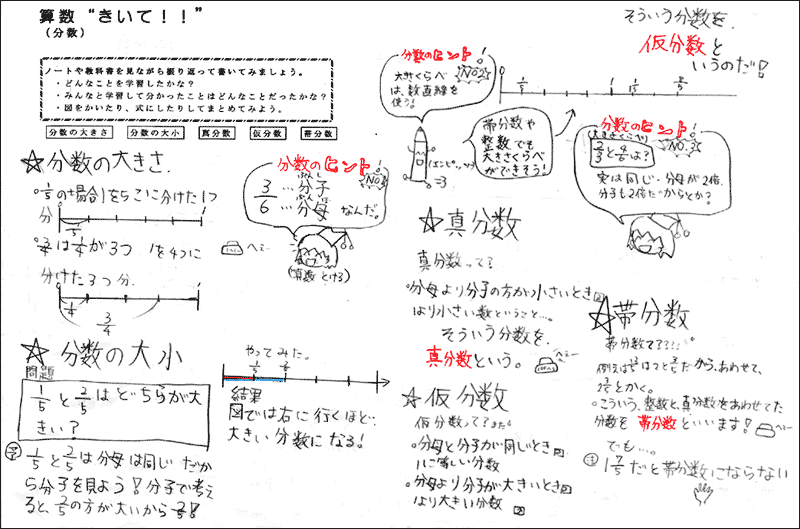



実践記録算数4年




小4算数 分数 の学習プリント 無料ダウンロード 印刷




小学3年生 算数 無料問題集 分数と小数の大小 おかわりドリル




小4の算数 分数の大きさ比べ 分母が大きいと小さいもの Youtube



小学数学五年级 分数大小的比较一 学习视频教程 腾讯课堂



3年算数分数のたし算ひき算 わかる教え方




分数ものさしありがとう 分数の直感的な理解が進みます ちくちくねっと




すきるまドリル 小学2年生 算数 わけた大きさ 分数 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



1




意外に複雑 分数の大小の見分け方6つのパターン 中学受験クルージング



一课研究之 分数大小比较的教材较研究 11月日




高校数学 累乗と累乗根の大小比較 受験の月



分数の大きさ比較ドリル




六年级奥数分数大小的比较 Doc 三九文库网




分数の大小 15秒以内に解けますか 一瞬戸惑う分数の大小 子供から大人まで動画で脳トレ 楽天ブログ



4年算数 分数 2 わかる教え方のポンイト



1
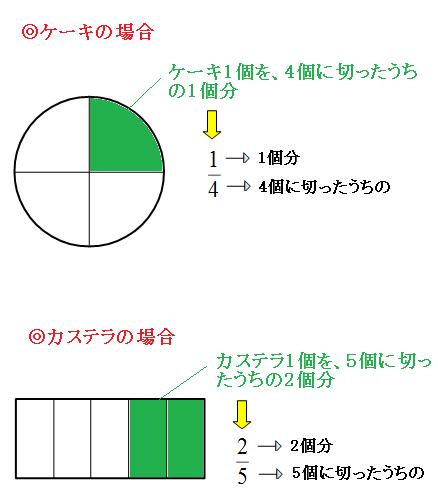



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利
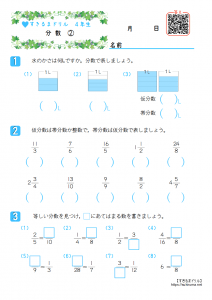



すきるまドリル 小学4年生 算数 分数 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント
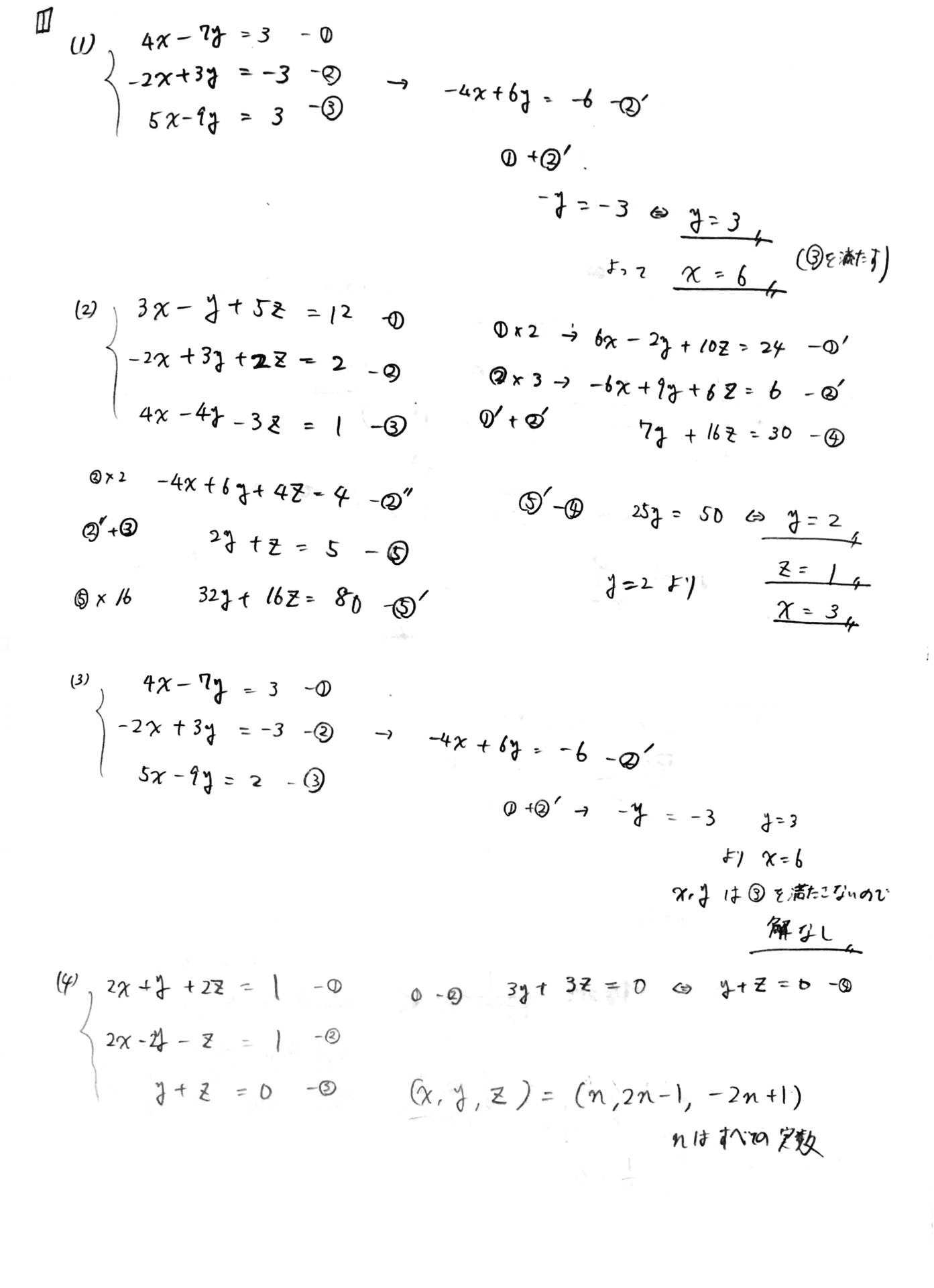



高校数学の復習 分数の大小比較 5 7 理系大学生が理系大学生に伝える例題集




分数 仮分数と帯分数の大きさ比べ 小4算数 無料プリント
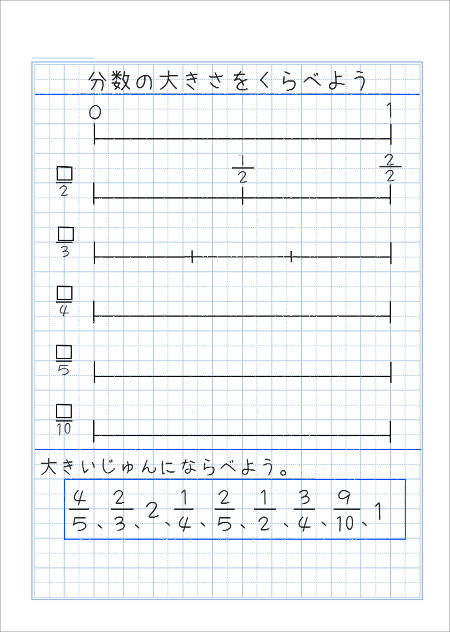



分数の大きさを比べよう 家庭学習レシピ



小升初数学重要考点之一 比较分数大小 有妙招




累乗根の大小です 2 たぶん分数の大小が分かっていないと思うのですが なぜ Clearnote
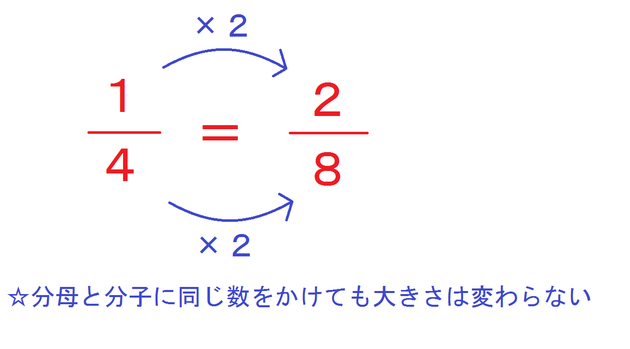



算数 本当に 分かる という事 分数の大小 通分 エース学院
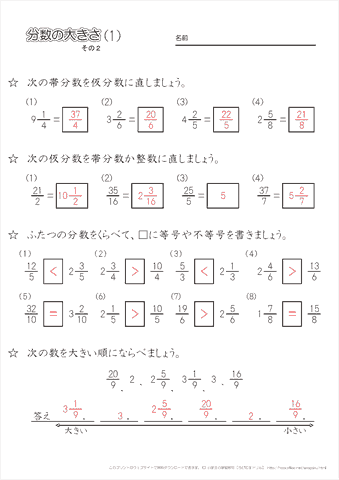



小学4年生の算数 分数の大きさ 2 真分数 仮分数 帯分数の計算 練習問題プリント ちびむすドリル 小学生
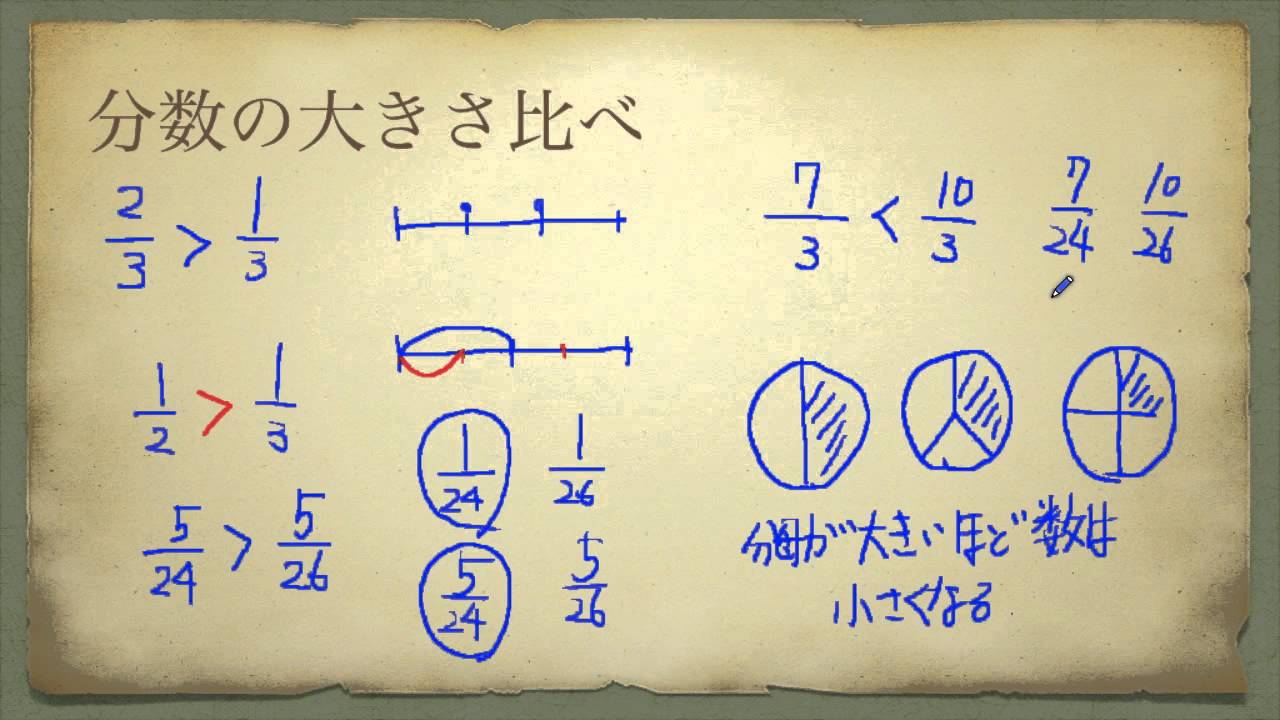



小学校4年 算数 分数の大きさ比べ Youtube



Www16 Sapporo C Ed Jp




4 52 分数 分数の大きさ
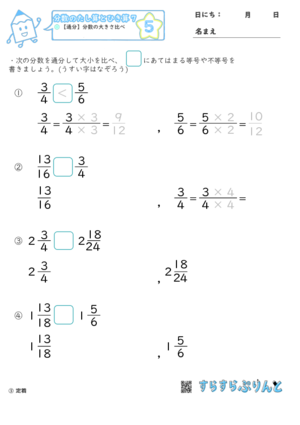



通分 分数の大きさ比べ 小学4年生算数 無料プリント教材



分数大小的比较方法 百度经验



分数の大小 浦和明の星女子中学 07年 筑波大学附属中学 09年 どう解く 中学受験算数




分数的大小比较 分数ppt课件 第一ppt



City Ota Tokyo Jp




分数怎么比大小 搜狗搜索



3年算数分数のたし算ひき算 わかる教え方




分数 仮分数と帯分数の大きさ比べ 小4算数 無料プリント
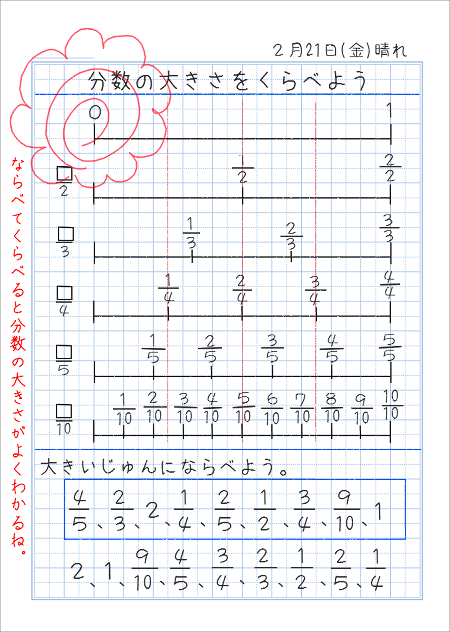



分数の大きさを比べよう 家庭学習レシピ



2 学習指導案



掌握这些方法 分数大小的比较才会确保不出错 每日头条




分数と小数の比べ方 直し方 変換 教え方 計算方法 元小学校教師が教える できる子ども育成塾 小岩 個別指導塾 小学生専門 国語と算数の苦手を克服
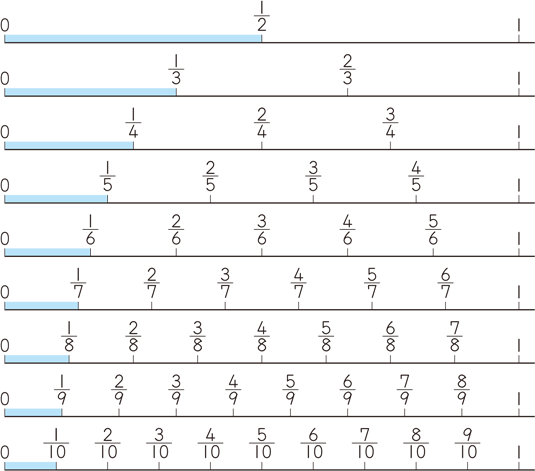



単位分数と分数の性質 算数用語集
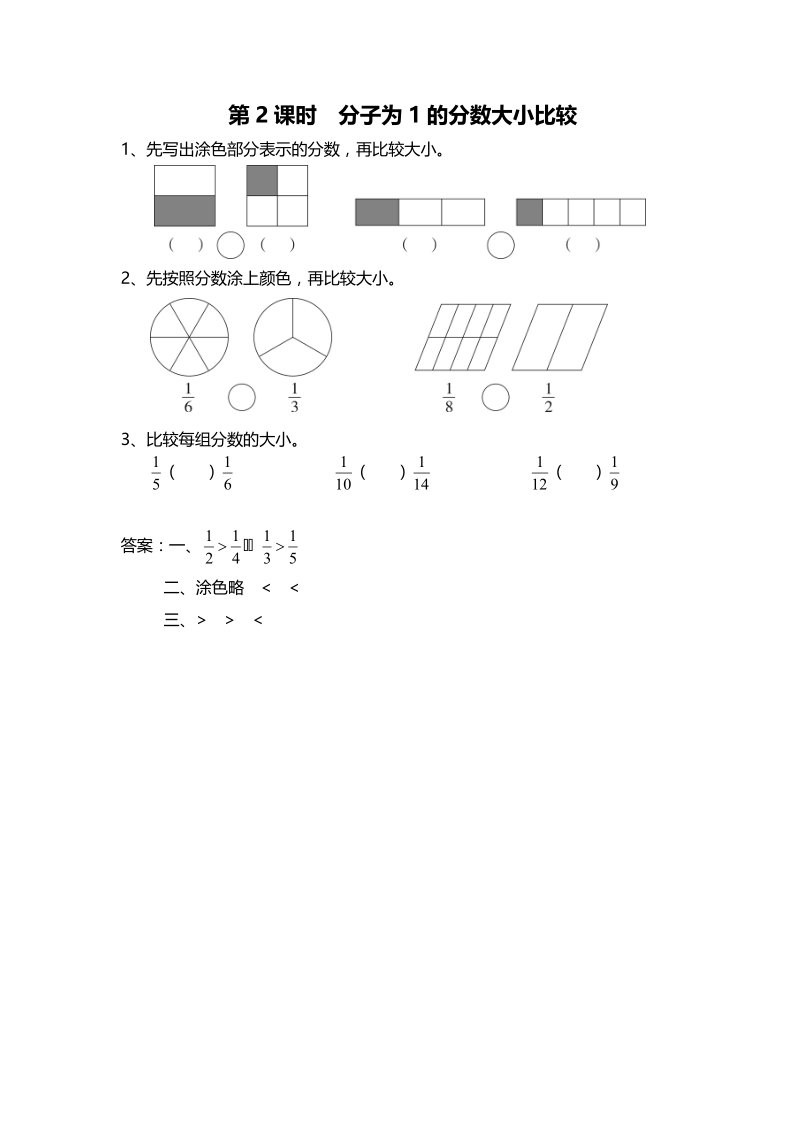



分子为1的分数大小比较 课时作业 含答案 七七文库www 77wenku Com




分数的大小 分数的意义ppt下载 牛二ppt



分数比大小 按照分数涂上正确的颜色并比较分数大小 红豆饭小学生简笔画大全



1




意外に複雑 分数の大小の見分け方6つのパターン 中学受験クルージング



分数比大小10字 范文118




正負の数 大小関係を不等号で表すためのポイントまとめ 数スタ



如何比较两个分数的大小 只会通分法 4种常用方法介绍




Qb説明 5年 分数のたし算 ひき算 On The App Store




ルートの大小関係の問題 の中の大きさに注目すれば簡単 中学や高校の数学の計算問題



2 分数的大小比较 一 Page7 浙教版五年级数学下册 新思维 电子课本 教材 教科书 好多电子课本网
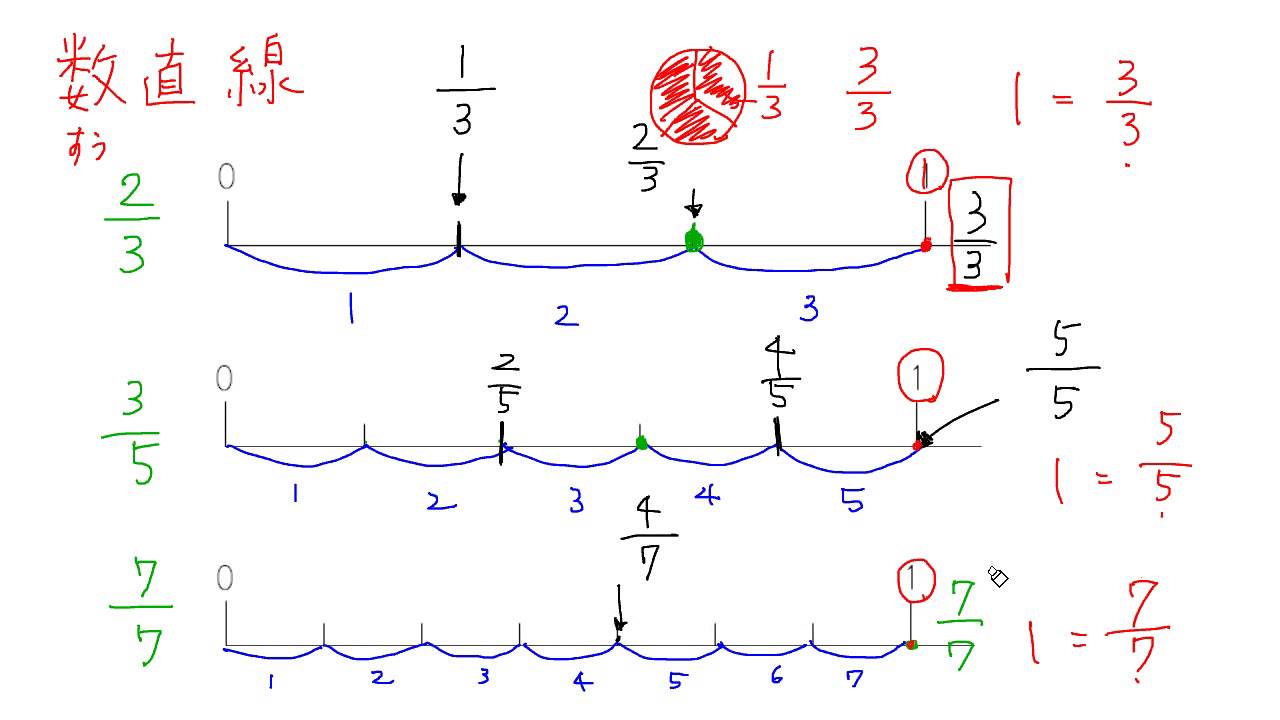



分数の大小 Youtube



头条问答 如何比较两个分数的大小 19个回答




大きさの等しい分数 スクールプレゼンター用教材 教材 プリント 学びの場 Com
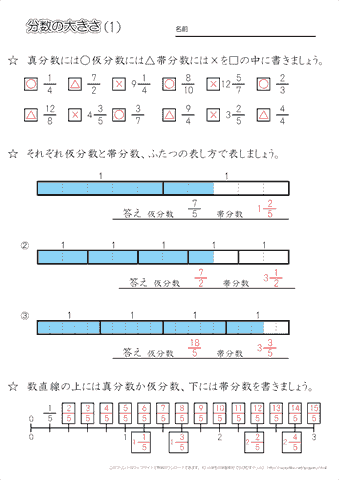



小学4年生の算数 分数の大きさ 1 真分数 仮分数 帯分数の意味 練習問題プリント ちびむすドリル 小学生



按照分数涂色并计算分数大小 红豆饭小学生简笔画大全




4年生算数ドリル 分数
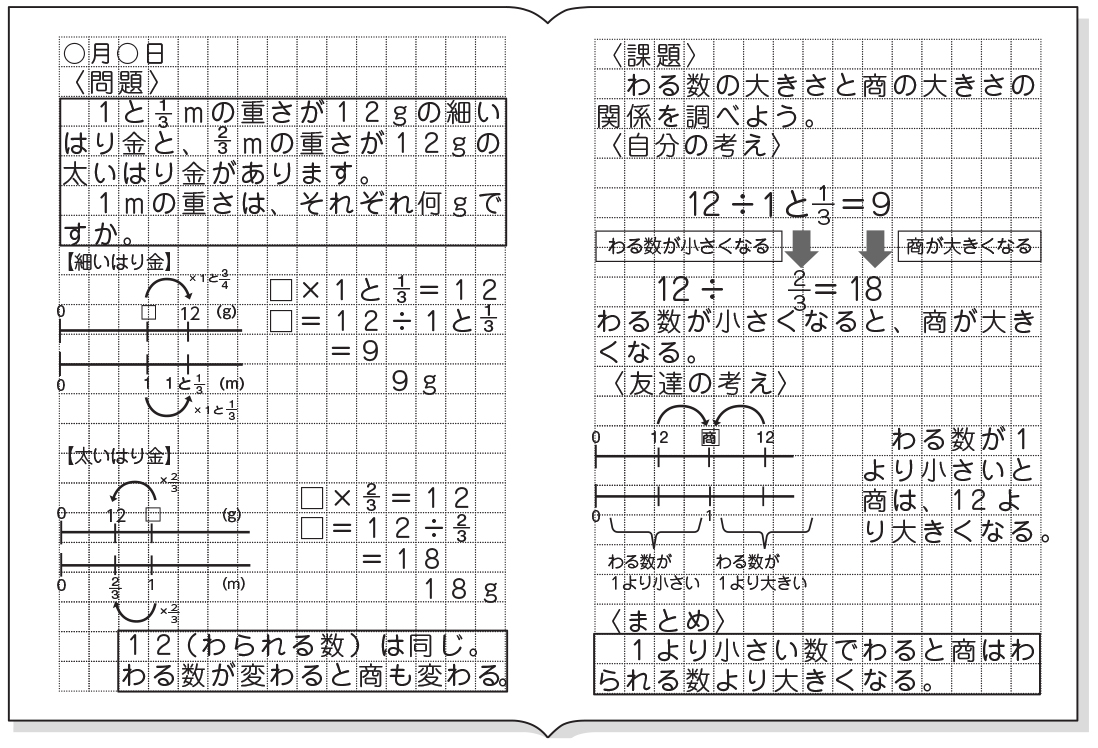



小6算数 分数のわり算 指導アイデア 2 みんなの教育技術
コメント
コメントを投稿